Introduction

Accelerated Life Testing (ALT) is a vital methodology used by manufacturers to estimate a product’s reliability under normal-use conditions by testing it at elevated stress levels. By exposing products to harsher environments—such as higher temperatures or voltages—failures occur more quickly, allowing for the extrapolation of lifetime data. This analysis uses statistical models to relate failure times under high-stress conditions to those expected at normal usage levels.

In this example, the Arrhenius life-stress model together with the Weibull distribution are used to model failure data under different stress levels. Arrhenius life-stress model is a single-stress model typically used when temperature is the accelerated stress.

Experimental Setup

An accelerated life test was conducted with temperature as the stress. Nine and six units were tested at 350 K and 450 K respectively. The test was suspended after 1200 hours.

The goal is to estimate the Weibull Probability Density Function (PDF) at 300 K, the intended use condition.

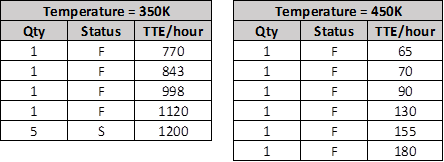
Resources_AltOverview1 — Figure 1: Time-to-Failure dataset at 2 temperature (stress) levels, 350 K and 450 K

For a single-stress test (in this case, temperature is the only stress), at least two stress levels are required. In general, for an experiment with N stresses, the minimum number of stress levels is N+1.

Life-Stress Relationship (LSR) Model

To extrapolate failure data from high-stress tests to normal-use conditions, a Life-Stress Relationship (LSR) model is needed. In this example, we use:

Arrhenius Model (for temperature stress)
Weibull Distribution (for time-to-failure)

The Arrhenius model is a widely-used single-stress LSR model for temperature-accelerated tests, and the Weibull distribution provides flexibility in modeling failure behaviors with its shape (β) and scale (η) parameters.

Resources_AltOverview2 — Figure 2: Tests are conducted at higher temperature levels (higher stress), and the PDF at used-level is induced using Life-Stress-Relationship (LSR) model

Detailed discussion on Life-Stress-Relationship is beyond the scope of this presentation. You can find more information from the book, Accelerated Testing: Statistical Models Test Plans and Data Analyses, by Wayne Nelson.

Verifying Distribution Assumptions

Accelerated Life Test Analysis assumes that the distribution shape parameters are the same across each experiment. Since the assumed underlying distribution is Weibull, we need to verify if the beta (shape parameter) remains constant from the experiments at 350K and 450K.

To check if both experiments have common beta (shape parameter) values, create a contour overlay plot. Create LDA worksheets for respective 350K and 450K datasets.

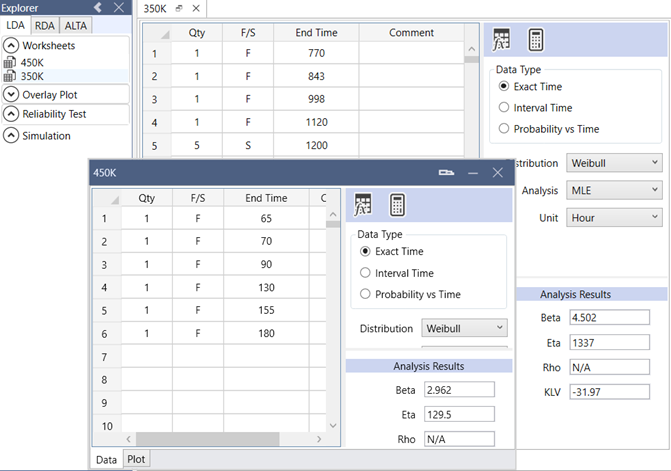
Resources_AltOverview3 — Figure 3: The Beta point-estimates for 350K and 450K datasets are 4.5 and 2.9 respectively

Tests are conducted at higher stress levels so that failures can be observed faster.

Add an Overlay Plot and set Plot Type to Contour plot.

Resources_AltOverview4 — Figure 4: Common beta range

From the contour plot, there is no evidence that the beta values are different. Hence, the assumption that 'shape parameters are the same across each experiment' is not violated.

So, now we can proceed to perform accelerated life test analysis.

Model Estimation and PDF Derivation

Using the Weibull Toolbox’s ALTA module, the following settings are applied:

LSR model: Arrhenius
Lifetime distribution: Weibull
Estimation method: Maximum Likelihood Estimation (MLE)

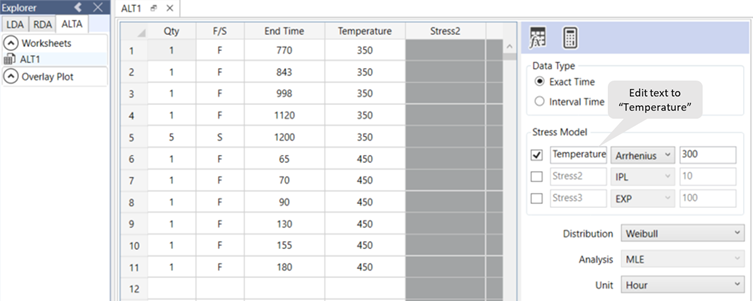
Resources_AltOverview5 — Figure 5: The Life-Stress Model and Distribution are set to Arrhenius and Weibull respectively

Given the models and data, Maximum likelihood estimation (MLE) solutions for the parameters are derived.

The Weibull PDF at 300K is:

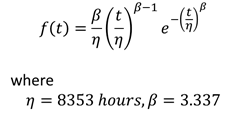
We can derive the reliability related plots at 300K:

Resources_AltOverview6 — Figure 6: Probability Weibull, Reliability vs Time, PDF, Acceleration Factor (AF) vs Stress plots (at 300K)

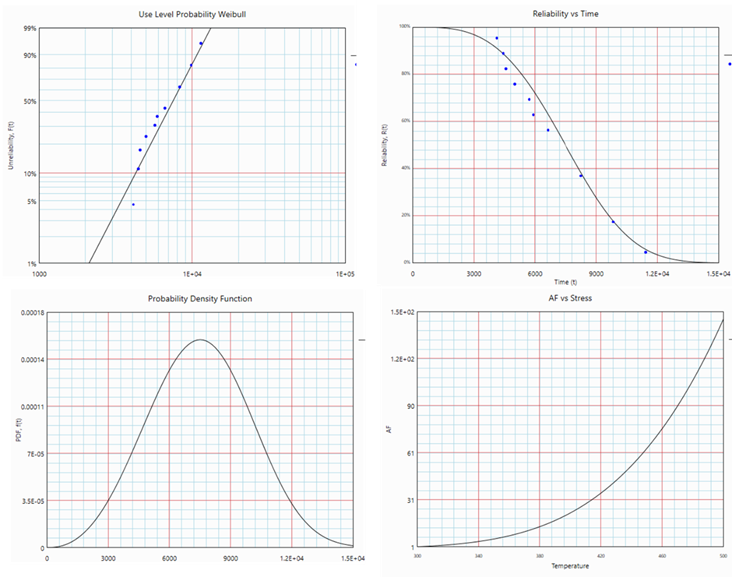
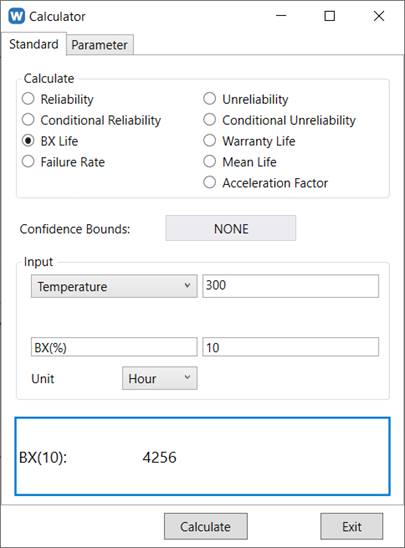
You can also obtain other reliability metrics from the ALTA Calculator, such as the B(10) life:

Conclusion

Most ALT experiments are conducted by manufacturers in order to complete the test faster, experiments are conducted at higher stress levels. The PDF under normal-use conditions is obtained by extrapolating from high-stress-level PDFs using a Life-Stress-Relationship (LSR) model.

To conduct an Accelerated Life Test (ALT) analysis, user needs to:

Identify the stress that can cause the units to failure faster.
Determine the Life-Stress-Relationship model associated to the stress.
Determine the underlying distribution.
Conduct the experiments at different stress levels (Designing the experiment is not discussed here) to obtain Time-To-Failure dataset.
Compute the ALT model parameters.

-End-